O USO DA HISTÓRIA NO ENSINO DE MATEMÁTICA

O uso da história no ensino de matemática

View more presentations from drikamendello.

ÓTIMAS NOTÍCIAS!!!

Estou feliz. Super feliz para ser sincera. O artigo que escrevemos intitulado "O uso da História no Ensino de Matemática: uma abordagem do Teorema de Pitágoras" será apresentado no ENCONTRO PARAENSE DE EDUCAÇÃO MATEMÁTICA - EPAEM. Se quiserem ler o aritgo, ele está postado no blog. É só ir lá no finalzinho da página, onde está "arquivos neste blog" e clicar nos arquivos de "outubro(2)", você verá os slides e o artigo.

Gostaria de agradecer a Msc. Jeane da Silva por ter esta iniciativa e nos incentivar a explorar a Educação Matemática. Muito obrigada professora!

Bom, quem estiver inscrito no EPAEM poderá assistir a essa grande vitória na Universidade da Amazônia - UNAMA, onde ocorrerá o evento. Endereço: Av. Alcindo Cacela, 287. Bairro Umarizal. Nossa apresentação será no bloco C sala 304 às 16:10hs. Data: 10/09/10. Ate lá!

Por Adrielle.

O QUE SE PODE FAZER DE HISTÓRIA NAS AULAS DE MATEMÁTICA?

Uma vertente pouco cultivada é a da História. Essencialmente, retratar, pelos seus próprios depoimentos, a vida e obra de matemáticos brasileiros. Além da valorização e do reconhecimento da contribuição de nossos conterrâneos à Matemática e à sua difusão aqui no Brasil, esse trabalho servirá para preservar a memória nacional, extremamente importante para os historiadores do futuro.

Nos países que foram berço de desenvolvimento matemático, uma prática interessante tem sido "Excursões Matemáticas" de cunho histórico. Por exemplo, visitas à casa onde nasceu Isaac Newton, à universidade onde estudou. Outra atividade é o levantamento de monumentos dedicados a um matemático célebre e também a iconografia. No Brasil esse material é paupérrimo. Mas há possibilidades. Por exemplo, uma excursão à Queluz, Em Portugal, onde há um pequeno museu de Malba Tahan, é muito interessante. Ou mesmo visita para reconhecimento de obras à bibliotecas públicas e privadas.

Mas há muita matemática feita por não matemáticos. Por exemplo, Fermat muitas vezes é chamado "o Príncipe dos Matemáticos amadores". Mas também é claro que há muita matemática implícita em obras não matemáticas, do dia-a-dia. Essa é uma das grandes lições que tiramos da História da Matemática. Muitas das grandes teorias matemáticas tem sua origem em práticas cotidianas.

SUGESTÕES PARA PROFESSORES

Qualquer indivíduo, durante todo o seu dia, calcula, mesmo sem se aperceber disso, tempo e espaço, e traça planos de ação. Identificar essa Matemática do cotidiano é algo que pode ser muito bem explorado pelos professores. É atual, interessante e útil.

Um outro exercício interessante, de natureza histórica, é o levantamento de fatos matemáticos numa comunidade. Desde o traçado da cidade (em alguns casos, as cidades brasileiras foram planejadas) até a construção e localização de monumentos. Os urbanistas, os arquitetos, os políticos e empresários, todos fizeram um estudo preliminar e um projeto para suas ações. Fizeram um modelo ou um planejamento, sempre repousando sobre uma análise matemática. Isto pode ser objeto de interessantes pesquisas.

Uma outra sugestão também de caráter histórico: escrever sobre professores secundários de matemática que marcaram uma escola ou mesmo uma comunidade. Se ainda vivos, entrevistá-los. Se já falecidos, entrevistar parentes, amigos, ex-alunos. A memória de matemáticos, de professores de matemática e de atividades matemáticas brasileiras é muito importante e deveria ter prioridade em cursos de História da Matemática. Dão excelentes e importantes temas para monografias, dissertações e teses, e mesmo temas para projetos de pesquisa para docentes e pesquisadores.

Mas voltemos às reflexões sobre o ensino da História da Matemática como ele é mais comumente entendida no mundo acadêmico. Está claro que não será possível a um professor de matemática explicar a origem histórica da matemática, mesmo que se restrinja a alguma sub-área específica. Essa é uma questão das mais desafiadoras. Muitas vezes se apresenta a História da Matemática no ensino como algo definitivo, insinuando "isso foi assim", o que pode ser falsificador. A História da Matemática no ensino deve ser encarada sobretudo pelo seu valor de motivação para a Matemática. Deve-se dar curiosidades, coisas interessantes e que poderão motivar alguns alunos. Outros alunos não se interessarão. Mas isso é natural.

Jamais deve-se dar a impressão, através de um desfilar de nomes, datas, resultados, casos, fatos, que se está ensinando a origem de resultados e teorias matemáticas. Sabe-se que as necessidades e as idéias vão se organizando ao longo da história, em tempos e lugares difíceis de serem localizados. Numa certa época, as idéias começam a se organizar, a tomar corpo, e a serem identificadas como isso ou aquilo. A partir daí entram para a "história". Mas não nasceram assim.

Outra maneira de se praticar história no ensino é fazer acompanhar cada ponto do currículo tradicional por uma explanação do contexto socio-econômico e cultural no qual aquela teoria ou prática se criou, como e porque se desenvolveu. Isso é muito freqüente nos cursos de história da matemática.

Para se adotar essa prática, a formação do professor é essencial. Nas boas licenciaturas há uma ou duas disciplinas de História da Matemática. Mas nem todo professor teve um curso de História da Matemática ou tem acesso a livros especializados. A preparação que permite ao professor fazer uma abordagem histórico-crítica exige um aprendizado permanente. Geralmente vem como resultado de ele ter feito as disciplinas tradicionais dos programas e de ter refletido sobre esses cursos, feito leituras e lido curiosidade sobre os conteúdos tradicionais. Insisto na palavra sobre. Não é necessário que ele conheça profundamente o tema para poder falar sobre o tema. Mas é importante que ele esteja preparado para dizer "Isso não sei" ou "Isso eu não consegui entender". Um professor que não for capaz de dizer isso para seus alunos será extremamente limitado, amedrontado e as suas aulas serão muito pobres e enganadoras.

O que seria uma preparação histórica básica, essencial, para todos os professores de Matemática? O que se encontra no Almanaque Abril 1995, pp.688-695 responde a essa pergunta. Ali há uma listagem cronológica de fatos e indivíduos que é o essencial na evolução da Matemática. O ideal, que é muito fácil de se conseguir, é acompanhar essa leitura com uma listagem cronológica dos grandes eventos internacionais, sempre acompanhando o exame dos fatos com a consulta a um Atlas -- que o próprio almanaque traz. Assim será possível localizar os lugares dos quais se está falando e o contexto internacional quando se deu o fato matemático. É interessante notar a forte concentração geográfica da produção matemática em certos períodos da história e como essa concentração se desloca.

Poucos professores conhecerão tudo o que é mencionado nessa história sintética e cronológica. Aparecerão nomes de indivíduos e referências a teorias sobre as quais o professor nunca ouviu falar antes. Isso pode ser uma motivação para que o professor tenha curiosidade de ver do que se trata. Caso ele não tenho acesso a livros mais especializados, ele pode consultar uma Enciclopédia, que é uma excelente fonte de informação. Ou pode, através da Internet, freqüentar algumas das inúmeras listas de discussão sobre a História da Matemática.

Também é muito interessante gastar um tempinho falando sobre as pessoas que estamos estudando. Por exemplo, sempre dando lugar e data de nascimento e de morte - se é que já morreu! Há muito material acessível sobre isso. Uma enciclopédia geralmente traz essas informações sobre os nomes mais importantes. Também os livros correntes de história da matemática têm essas informações. Em particular os livros de Carl B. Boyer, Howard Eves e de Dirk Struik.

Veja a versão completa deste artigo em Interface entre História e Matemática

UM POUCO DA HISTÓRIA DO JOGO SUDOKU

Todos devem ter visto na barra lateral que colocamos o jogo Sudoku para divertir os nossos visitantes... E como sugestão do professor Everaldo, que visitou nosso blog e deu a dica, postamos agora um resumo da história do sudoku e como jogá-lo.

O sudoku não é um passatempo antigo que só agora foi descoberto ou divulgado. Sudoku é uma palavra japonesa que significa “números que devem estar sós”. No Japão, este puzzle tornou-se popular em 1986, mas só em 2005 se popularizou internacionalmente. A palavra “sudoku” é uma marca registada pelo editor de puzzles japonês Nikoli, Co., mas o puzzle foi criado por Howard Garnes em 1979, em Nova Iorque. Mas, são os “quadrados mágicos” do matemático suíço Euler, (1707-1783) que estão na base do conceito do sudoku !

Em 1989, um editor de jogos de computador fez a sua versão e não demorou muito que surgissem programas informáticos que gerassem sudokus. Os puzzles sudoku apareceram pela primeira vez no jornal a 12 de Novembro de 2004, no The Times.Logo outros jornais o seguiram, com outros criadores de sudokus e alastrou-se a todo o mundo, em papel, no computador, no telemóvel...

O que é o sudoku ? Como se faz ?
Um sudoku é um puzzle em que se têm de preencher as casa vazias com algarismos de 1 a 9, de modo a que o mesmo algarismo não se repita em cada linha, coluna e quadrado. Um puzzle sudoku tem a ver com a lógica e não com conhecimentos de matemática. Para facilitar a resolução de um sudoku deve procurar-se para cada casa quais os números que a podem ocupar – que são os que não aparecem já na linha, coluna e quadrados que correspondem a esse bloco. Nas casas em que só surgem um número, esse é o certo e definitivo, depois é prosseguir com o mesmo processo.  Só há uma solução para cada puzzle sudoku.

Para saber mais detalhes sobre o tutorial do Sudoku clique aqui.

UMA BREVE VIAGEM NA HISTÓRIA DA MATEMÁTICA

2.000 a.C.

Os babilônios criam as primeiras formas de numeração posicional, ou seja, um número pode ter diferentes valores, dependendo da posição em que estáSéc. 6º a.C. Os gregos simplificam notação numérica, abandonam as formas gráficas do número e as substituem por letras, que correspondem à designação inicial de número (acrofonia). O número 100, por exemplo, era a letra H (de Hekaton = cem).

Séc. III a.C.

Euclides, o maior matemático da Antiguidade, estrutura o conhecimento matemático.

Séc. V

Os hindus criam um sistema de numeração que reúne o uso do zero, o princípio de posição e a base 10, criando o sistema até hoje utilizado.

Séc. VIII

Depois das Cruzadas, o matemático e comerciante Leonardo de Pisa leva para a Europa o sistema indo-arábico, que impulsiona o desenvolvimento do mercantilismo. Começam a chegar livros árabes, provocando reações da igreja, contra o sistema "herege".

Séc. XIV

Grande produção dos matemáticos a partir dos livros árabes de matemática. O sistema indo-arábico vira coqueluche entre comerciantes por sua praticidade.

Séc. XVI e XVII

Estudos da matemática entrelaçam-se com a filosofia (Descartes) e com os avanços da física (Galileu). Aparecem os cálculos com logaritmos, por exemplo.

Séc. XVIII

Momento decisivo da matemática moderna, com a publicação de "Princípios Matemáticos da Filosofia Natural", de Isaac Newton. Surgem novas conceituações da matemática. Começa a ser formulada a teoria das funções.

Séc. XX

Surgem novos conceitos da matemática, principalmente a partir das teorias formuladas na física por Albert Einstein e Max Planc, nas áreas da física quântica e da relatividade. A partir do final da Segunda Guerra Mundial, surgem a teoria dos fractais e a teoria dos jogos.

HISTÓRIA DA MATEMÁTICA NA EDUCAÇÃO

História Da MatemáTica na Educação

View more presentations from Juaumath_20.

O USO DA HISTÓRIA NO ENSINO DE MATEMÁTICA: UMA ABORDAGEM DO TEOREMA DE PITÁGORAS.

Adrielle Cristine Mendello Lopes

Graduanda em Licenciatura Plena em Matemática (UEPA)

E-mail: drika.mendello@gmail.com

Ana Paula Cardoso

Graduanda em Licenciatura Plena em Matemática (UEPA) e Pedagogia (UFPA)

E-mail: pittypaula@hotmail.com

João Paulo da Silva Cardoso

Graduando em Licenciatura Plena em Matemática (UEPA)

E-mail: juaum18@gmail.com

RESUMO: A educação matemática surgiu para contribuir com ensino da matemática por meio de suas tendências, neste sentido analisaremos o uso da história no ensino de matemática abordando como esta tendência auxilia no processo de ensino-aprendizagem do educando no assunto pertinente ao Teorema de Pitágoras, seja por metodologias baseadas em leitura de textos históricos ou por demonstrações realizadas.

Palavras-Chaves: História da matemática, Teorema de Pitágoras, Aprendizagem e Leitura.

EDUCAÇÃO MATEMÁTICA E A HISTÓRIA DA MATEMÁTICA

     A Educação Matemática surgiu com a idéia de estudar e construir princípios da relação da prática pedagógica do ensino de matemática. Neste sentido entendemos quando Siqueira (2007) fala que este tema apresenta algumas tendências pedagógicas, como a história da matemática que tem por fim auxiliar o processo de ensino-aprendizagem e o interesse dos alunos.

     Nesta perspectiva, este trabalho tem por objetivo analisar de maneira geral, o uso da história no ensino de matemática de nas suas diversas relações, e especificamente o ensino do Teorema de Pitágora com o auxílio da história da matemática. E também, discutir como este tema pode auxiliar as instituições de ensino a romper a ideologia que a matemática é uma ciência que a maioria das pessoas não consegue aprender por ser abstrata.

     A história da matemática é um dos elementos fundamentais que envolvem leitura e matemática. Os Parâmetros Curriculares Nacionais de Matemática de 5° a 8° séries (1998) indicam o uso da história no ensino da matemática sendo uma forma dos alunos aprenderem os conceitos matemáticos por meio do passado e do presente, compreendendo assim a construção de diversas fórmulas na matemática.

     Deste modo verificamos a importância do uso da história no ensino da matemática, pois segundo Freire (1996) explica que formar é muito mais que realizar a prática da educação bancária que apenas treina o educando, mas é acima de tudo buscar novas metodologias de ensino para que a sala de aula de matemática torne-se um local de investigação, produção de conhecimentos e de experiências.

     Sendo assim, o uso da história da matemática é fundamentalpara as práticas pedagógicas na sala de aula de matemática, pelo fato de o sentido dos fatos matemáticos estarem presentes na realidade dos alunos.

A HISTÓRIA E OS SEUS OBJETIVOS

     O homem relaciona-se com a matemática desde o princípio da humanidade, com o objetivo de estimar quantidades, sejam elas animais, frutas, pedras, enfim tudo aquilo que for da vivência dele na visão de Miorim (1998). Como percebemos a história nos remete a narração de fatos e acontecimentos ocorridos.

     Neste contexto podemos analisar que a construções dos conceitos matemáticos prontos e acabados surgiram de um longo processo histórico, e que como cita Siqueira (2007):

   “Conhecendo a História da Matemática é possível perceber que as teorias que hoje aparecem acabadas e elegantes resultaram sempre de desafios que os matemáticos enfrentaram, que foram desenvolvidas com grande esforço e, quase sempre, numa ordem bem diferente daquela em que são apresentadas após todo o processo de descoberta.” (Siqueira, 2007, pág. 26).

    Com esta análise, o educando vai passar a perceber que a matemática passou por diversas transformações ao longo do processo histórico, compostas de erros e acertos, e não como verdades absolutas. Desta forma, passa a ser uma disciplina significativa.

     A esse propósito, Mendes (2001, pág. 34) destaca que “À medida que busca compreender a realidade histórica na atividade investigatória, o aluno estará construindo para si, informações matemáticas contidas na realidade investigada”. Segundo estas idéias o educando passará a ter uma postura critica e reflexiva.

     Conforme explica Fonseca e Cardoso (2005), para poder interpretar os problemas matemáticos, o aluno precisa acima de tudo compreender do que ser trata o texto, em uma linguagem clara e coerente. Para ele ter esta compreensão é preciso que a leitura e a compreensão de textos sejam muito bem trabalhadas nas aulas, seja ela de matemática ou de língua portuguesa.

     Contudo, compreendemos quando Mendes (2001) fala que os livros didáticos de matemática muito pouco ou nada apresentam assuntos relacionados a história da matemática, reduzidos a biografia de célebres matemáticos, fato este que comprova o não interesse de muitos autores pelas tendências da educação matemática.

     Mas o professor por ter um papel importantíssimo na sala de aula, deve elaborar atividades que explorem ao máximo metodologias de ensino que envolva a história no uso da matemática. Como, por exemplo, leituras paradidáticas como o volume “Contando a história da matemática” de Guelli (1995) ao qual mostra informações a respeito das noções do triângulo retângulo e as idéias Pitagóricas despertando a reflexão do pensamento matemático no aluno.

     A este respeito a leitura de textos em aulas de matemática buscam fazer com que os alunos construam um novo olhar para a linguagem matemática. Um olhar que não seja preso a metodologias que estejam agarradas a álgebra pura ou a cálculos que muitas vezes só professores e poucos “bons alunos” conseguem resolver.

A HISTÓRIA DO TEOREMA DE PITÁGORAS E O SEU ENSINO

     De acordo com Eves (2004) o Teorema de Pitágoras não foi descoberto por Pitagóras, mas talvez por matemáticos que estudavam em sua escola Pitágora. Contudo, o que se sabe que o Teorema que foi demosntrado a apartir de dois quadrados, mas antes mesmo da primeira demonstração ( ver figira 1) este teorema já era conhecido por Babilônios há centenas de anos atrás e também pelos chineses por volta do ano 200 a.c.

Figura 1:Primeira demonstração do Teorema de Pitagóras

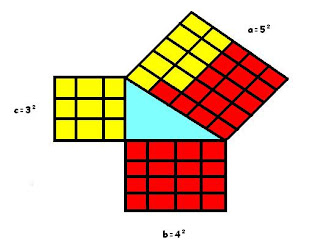
     Após esta demonstração muitas outras surgiram, entratando não é o objetivo deste trabalho analisar todas, mas a pertinente ao 6° ano do Ensino Fundamental, que corresponde ao enunciado “a área do quadrado sobre a hipotenusa de um triângulo retângulo é igual à soma das áreas dos quadrados sobre os catetos.” Ver figura 2.

Figura 2: Demosntração do Teorema de Pitagóras por meio da área.

     Analisando a importância do Teorema de Pitágoras no dia-a-dia, ele pode ser aplicado para calcular a inclinação da rampa de um telhado ou o raio aproximado da terra, ou também para fixar exatamente o ângulo de 90º entre duas paredes a serem construídas.

PROPOSTA DE ATIVIDADE EM SALA DE AULA

    Os Paramêntros Curriculares Nacionais de Matemática de 5° a 8° séries(1998, pág. 89) sugere “verificações experimentais, aplicações e demonstração do teorema de Pitágoras.”

     Neste contexto, o professor deve inicialmente analisar a realidade em que seus alunos estão inseridos e posteriormente planejar as ações metodológicas a serem utilizado nas salas de aula. Por isso se faz necessário que ele compreenda a história da matemática que irá ensinar aos seus alunos, conforme mostra Mendes (2001).

    “Acreditamos que a partir do uso das atividades é possível alcançar os objetivos previstos no programa de ensino, desde que cada professor saiba utilizá-las durante suas aulas, organizando de maneira formal, todo o conteúdo programático, até desencadear em uma série de exercícios de fixação de conteúdo, sempre apoiando nas informações iniciais.” (Mendes 2001. Pág. 69).

    Essas ações metodológicas necessitam ser bem trabalhadas para fixação do conteúdo pois também perpassam pela relação ensino - aprendizagem. Mas para trabalhar com total eficiência a metodologia é necessário que o educador tenha um domínio do conteúdo e da história do Teorema de Pitágoras para poder responder a prováveis questionamentos que poderão ocorrer no decorrer a aplicação metodológica, caso contrário o aluno pode perder o interesse pela proposta apresentada ou até mesmo ficar sem entendê-la, o que não é seu objetivo.

     Com esta análise sugerimos que o ensino deste assunto por meio de sua história e aplicações prática, como por exemplo o professor sugerir para os seus alunos leituras que envolvam essa descoberta do teorema para que deste modo os educandos familiarizem-se com o assunto em questão.

    Com o embasamento histórico e teorico o professor deve posteriomente sugerir aos seus alunos que construam o teorema igualmente a figura 2, e em seguida de modo que cada quadrado seja exatamente igual um ao outro. Logo após, os quadrados da área c e b serão recortados um a um.Posteriormente o professor pedirá aos seus alunos que encaixem os quadrados cortados em cima dos quadrados do lado a.

    Nesta perspectiva, o aluno poderá compreender como o Teorema de Pitagóras foi desenvolvido, e como ele pode ser demonstrado por meio de sua área, confirmando desta maneira o enunciado “ a soma dos quadrados dos catetos é igual o quadrado da hipotunusa”, ou seja, a²= b² + c². Oliveira (2008) sugere que nas atividades metodológicas, o aluno será convidado a decompor os quadrados construídos sobre os catetos em alguns pedaços e depois reagrupar essas peças exatamente sobre o quadrado construído sobre a hipotenusa.

     Sendo assim de acordo com D’Ambrósio (1996) “a história da matemática é um elemento fundamental para se perceber como a teoria e a prática da matemática foram criadas.”

  

CONSIDERAÇÕES FINAIS

     O processo de ensino – aprendizagem necessita de um elo transmissor que é o professor, sobretudo no aspecto da história da matemática.É importante deixar claro a formação e domínio do professor para passar com clareza as informações necessárias como compreender o processo de abstração, principalmente na matemática pois, como já dito no inicio desse artigo, muitas pessoas não conseguem aprender matemática e suas diversas relações por ser abstrata.

    Com esta análise, a aprendizagem significativa vai muito além de passar meros conteúdos em sala de aula, mas passa pelo processo de pesquisa, investigação e relação com a realidade a que alunos e professores estão inseridos. A partir destas idéias levantamos a bandeira de novas metodologias de ensino, não só para o Teorema de Pitagóras, mas para os conteúdos de matemática em geral que podem ser compreendidos de uma forma lúdico, histórica e lógica.

REFERÊNCIAS:

BICUDO, Maria Aparecida Viggiane. Pesquisa em Educação Matemática: concepções & perspectivas. São Paulo: Editora UNESP, 1999.

BRASIL. Secretaria de Educação Fundamental. Parâmetros curriculares nacionais : Matemática /Secretaria de Educação Fundamental . Brasília : MEC /SEF, 1998.

COSTA, R. A; ZUIN, E. S. L. O “teorema de pitágoras” sob uma perspectiva histórica: uma análise de livros didáticos de matemática do ensino fundamental no Brasil Disponível em:http://www.sbem.com.br/files/ix_enem/Comunicacao_Cientifica/Trabalhos/CC03188585683T.doc. Acesso em 19/09/2009.

D’AMBRÓSIO, Ubiratan, 1932. Educação matemática: da teoria a prática. Campinas, SP. Papirus, 1996. – ( Coleção Perspectivas em Educação Matemática ).

EVES, Howard. Introdução à história da matemática. Campinas, SP. Editora da UNICAMP, 2004.

FREIRE, Paulo. Pedagogia da autonomia: saberes necessários à prática educativa. São Paulo: Paz e Terra, 1996.

FONSECA, Maria da C.F.R.; CARDOSO, Cleusa de A. - em Lopes, Celli A. E. Escritas e leituras na educação matemática. Belo Horizonte: Autêntica, 2005.

IEZZI, Gelson, 1939. Fundamentos da matemática elementar, 3 : trigonometria – 8. Ed. – São Paulo : Atual, 2004.

GUELLI, O. Dando corda a geometria. São Paulo: Ática, 1995. (Série: Contando a História da matemática).

MENDES, Iran Abreu. O uso da história no ensino de matemática: reflexões teóricas e experiências. Belém: EDUEPA, 2001.

MIORIM, Maria Ângela. Introdução a história da Educação Matemática. São Paulo: Atual, 1998.

OLIVEIRA. J, A. Teorema de Pitagóras. Belo Horizonte. 2008. Disponível em http://www.mat.ufmg.br/~espec/monografiasPdf/Monografia_Juliane.pdf. Acesso em 19/09/2009.

TENÓRIO, R. M. (org.). Aprendendo pelas raízes: alguns caminhos da matemática na história. Salvador: Centro Editorial e Didático da UFBA, 1995.

SIQUEIRA, Regiane Aparecida Nunes de. Tendências da educação matemática na formação de professores / Regiane .Aparecida Nunes de Siqueira. -- Ponta Grossa: [s.n.], 2007.

DEVE-SE COMENTAR A HISTÓRIA COMO SE A MATEMÁTICA FOSSE SEMPRE ALGO BOM?

O uso da História da Matemática tem que ser um recurso para a motivação de aulas de matemática, porém quando o professor descreve algumas passagens da história da matemática deve ter cuidado de não extrapolar em sua opinião.

De acordo com Aristóteles, os humanos são caracterizados pela racionalidade. A partir dessa hipótese não é difícil de se construir um argumento para a conclusão de que qualquer avanço no racionalismo é muito bom para a humanidade.

Porém esse não é o momento para decidir a importância e a boa qualidade relativas à matemática, mas é o momento para se observar um exemplo onde a exaltação da matemática introduz com freqüência tendências nos livros texto de História da Matemática. Este é o caso de Hipátia, uma matemática do século V que foi assassinada por uma quadrilha de rua na Alexandria. Hipátia era uma pagã, e alguns membros da quadrilha eram “cristãos”.

O professor que não gosta de matemática poderia descrever a morte de Hipátia como a remoção de uma reacionária arrogante que esta no caminho da nova sociedade cristã. Contudo, o professor que gosta matemática, invariavelmente, beatifica Hipátia lamentando sua morte como um sinal do declínio da Razão no Ocidente.

Aqueles que depositam um alto valor na matemática são tentados a julgar uma cultura em termos do número de teoremas que ela provou. Isso conduz a uma visão irrealista das culturas, como por exemplo, a antiga cultura chinesa, que não produziu muitos teoremas, mas que produziu algumas poesias e filosofias excelentes. Um professor que fala sobre a história da matemática, devidamente equilibrado, reconheceria a importância de muitas formas de atividade intelectual.

VEJA ESTES VÍDEOS

SUGESTÕES DE LEITURA